A letter to a dear friend: Quantum Physics and Time Travel
Dear ####,
Find attached a very long ramble through all of physics (it's Greatest Hits, kind of), that does eventually try and address your question regarding time travel, but with a slight overindulgence on the background and context of the question for you sir. Good luck... (Note I wrote most of this in the wee hours of the morning so don't treat it as gospel. just sayin...)
Find attached a very long ramble through all of physics (it's Greatest Hits, kind of), that does eventually try and address your question regarding time travel, but with a slight overindulgence on the background and context of the question for you sir. Good luck... (Note I wrote most of this in the wee hours of the morning so don't treat it as gospel. just sayin...)
Quantum Stuff
Quantum Mechanics says that particles are represented as a probability distribution known as a wavefunction. When I say the particles are represented by… I mean that all attributes (or properties) of the particle are basically determined by the same principle as rolling a bunch of dice.
 |
| Fig 1: Probability Distribution of the position (as a scalar) of a quantum wavefunction |
In fact, all properties of the particle are described like this – the figure above is for the position, and there is a similar distribution for the speed of the particle.
This basically reflects the fact that you cannot predict for sure what the position of a particle will be, even if you know everything about it right beforehand. You can measure the speed or position at an instant in time, but when you measure one you cannot measure or know the other (Heisenberg Uncertainty Principle). Anyway, that’s a quick intro to Quantum Mechanics – and a demonstration that Quantum stuff is alllllll based on probability distributions. There is no concrete information known at any particular time.
As these distributions show, a particle can be in any state described by the curve – although some states are more likely than others. A concept implied here is that if you have a large enough number of particles with the same probability distributions (wavefunctions), you CAN fairly safely predict their behaviour en masse – probability turns into reality as you increase the number of times a given probability is tested (the more coins you flip, over time (eventually) the closer you will get to 50% heads and 50% tails). This is the basis of a field of physics called statistical mechanics, that I shan't go into, that describes the large scale (macroscopic) behaviour of many particles together – i.e. their emergent behaviour.
Now comes the idea of quantum fields. Quantum Field Theory. This is where Einstein’s Theory of Relativity meets Quantum Mechanics, and things get even weirder. If you think about what I just said about Quantum Mechanics, it means that a particle’s properties can vary wildly over a small period of time (although this is less likelyto occur than for it to stay relatively near the centre of the distribution, extreme cases of behaviour can – and will, given enough particles, happen). Outliers – they exist in every field, the statistical anomalies that make some of the most interesting things in life happen, and the freakiest.
Einstein’s ToR tells us mass is equivalent to energy (E=mc2). That’s quite a thing to say actually, but we can get into that another time… Now, as these particles are moving around and their properties are changing – the grand (aggregate) sort of ‘overall quantity’ that is changing is their energy. Energy is probably the most abstract concept in Physics when you really get into it, but it can be expressed, or manifested in many ways –as speed (Kinetic Energy = ½mv2) and mass (E=mc2), generally. Combining these two equations together we can see that if an object had a known, finite amount of energy (say, a car), then it could either move faster and be less massive (I hate that phrase ‘less massive’ but it’s a very scientist thing to say – because more mass doesn’t necessarily make something bigger, it could just become more dense and take up the same amount of space. It would ‘weigh’ more though in an everyday environment – as the weight of something depends on the gravity and the mass (weight = mass * gravity)), or move slower and be more massive, or stop entirely and be at maximum possible mass.
Now, Quantum Mechanics shows us that these particles do not have a finite energy, it changes according to a wavefunction, and according to Einstein’s ToR, a certain amount of energy is equivalent to a certain amount of mass. Here comes the hard part (haha) – for any particle to exist, it must have a certain requisite amount of energy – this minimum required energy is known as the particle’s ‘ground state’. This can be looked at from a different perspective, however: the particle only exists because there happened to be enough energy in the right place at the right time, and could quite easily blink out of existence if its energy fell below its ground state. This is the idea behind Quantum Field Theory – that all particles are entities (science term is ‘local excitations’) of energy that exist within a fluctuating quantum field, and that they can blink in and out of existence at any time (I should probably mention that a particle is always ‘created’ with its antiparticle in this way, which is absolutely fine as they balance each other out in every way so the maths and all the concepts described still make sense… lol). This is the ephemeral nature of the Universe as described by Quantum Physics.
Topical note – this ‘quantum field’ that I just mentioned happens to be the Higgs field, and the mechanism by which particles possess mass is known as the Higgs mechanism. This is part of the Standard Model – the current ‘standard’ model of particle physics, which does quite well apart from the whole theory of gravitation thing (they are incompatible). The Higgs boson is a huge elementary particle that gives other elementary particles (except the photon and the gluon) mass. Quantum Mechanics tells us that big particles are likely to decay into smaller ones when they interact with other particles, the likelihood depends on the mass of the particle and the strength of the interaction. The Higgs boson is ultra mega big for a fundamental particle, and as it interacts with all other particles (giving them mass) it decays ridiculously fast which is why it’s so difficult to detect. Just realised I misleadingly said it interacts with all other particles, when it can actually interact with itself.
Now, Tachyons. Important first thing: there are actually two definitions of Tachyon - the original meaning (from the original paper written by a guy called Feinburg in 1967 where he coined the name) is that a Tachyon is a fundamental particle that can move faster than the speed of light (in a quantum field with 'imaginary mass'). This was very quickly shown NOT to happen. The model proposed did not allow this - instead, an imaginary mass causes an instability, leading to something called tachyon condensation.
When physicists talk about Tachyons today, they are actually talking about the 'quantum field with imaginary mass', NOT the particle that can move faster than light. This has clearly not been taken on board by Hollywood, even 45 years later. They are important in physics today – in fact the Higgs field is a Tachyon field, as it has an imaginary mass. According to the model proposed in 1968 – ‘excitations’ (particles – named Tachyons back then) in this field would propagate faster than the speed of light, but it was quickly realised that these excitations would not create local particles – and that the negative mass would cause an instability called Tachyon Condensation. This is closely linked to a topic called Spontaneous Symmetry Breaking that I wasn’t go into as it is a tricky one, but I’ll try and sum it up quickly so you have some overall picture.
The Standard Model tells us there are 4 fundamental forces (as we are taught in school) – Strong, Weak, Electromagnetic and Gravity. Just how until 1873 the electric force and the magnetic force were thought to be separate forces, until Maxwell demonstrated they were in fact one and the same (absolute breakthrough), particle physics tells us of something called the Electroweak Interaction. This states that at a high enough energy (called the unification energy: ~100GeV), the Electromagnetic and the Weak force unify into a combined Electroweak force. This force acts symmetrically on all fundamental particles. However, as the energy lowers (such as after the big bang, until now (apart from in particle accelerators)) the symmetry spontaneously breaks at around 80GeV and the forces start displaying different behaviour. Spontaneous Symmetry Breaking in general is where equations of motion obey symmetries, but at the lowest energy solutions, they don’t. An analogy I read is to consider the bottom of a wine bottle (suppose we’ll have to keep this one as a thought experiment now haha), it’s curved dome. If you balance a ball on it, it is symmetrical no matter how you rotate the bottle, but it could spontaneously fall down into the trough, and the symmetry is broken between the bottle and the ball (note: they themselves both remain symmetrical). This concept exists throughout physics – in an abstract way (think of it as one perspective), state changes of matter – e.g. water turning into ice. Many theories in physics are known as Gauge theories, this is where a change in the motion or inertia of a reference frame has no bearing on what is inside the reference frame. Imagine a train carriage, and you playing catch with a ball with some Canadian dude across the aisle, and then the carriage turns 90 degrees. If you also flip the coordinates 90 degrees (i.e. the Earth also moved 90 degrees underneath the train), then the properties of the tennis ball remain unchanged, and global symmetry is achieved, this is called a gauge transformation and is seen in things like Quantum Electrodynamics (QED). However, in real-life (the ‘macro world’) there aren't many situations like this, in the train carriage example, the Earth remains how it is, geometrically speaking, in relation to the carriage, and some serious shit goes down. The ball, however, maintains local symmetry (with itself). Global symmetry is not maintained, it is the reason for the Coriolis effect, and why planes don’t actually fly on constant bearings over long distances.
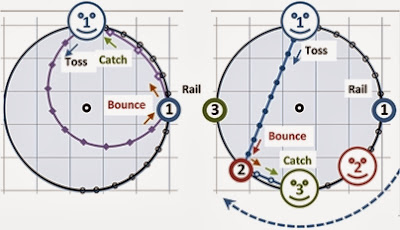
Consider this figure – you’re playing catch again, but this time on a carousel (rotating clockwise) and yourself! Both pictures show the SAME event, but from different perspectives (known as) reference frames). It’s a bit confusing at first, but I think you’re probably gonna have to bounce it off the wall at some point.
[Smiley Face(1)] (You), can account for the effect of the constant change of inertia of the reference frame by throwing the ball in a calculated manner ahead of where the receiver (you) currently is(are, lol, grammar in these situations gets srange). The left hand side Is showing you a bird’s eye view of what it looks like if the observer (webcam put on the top of the rotating middle pole of the carousel so the ‘circus folk’ can stare down girls tops) was moving WITH the carousel. The right hand side shows the same thing but where the observer (webcam stuck to the roof – probably more likely) is fixed. Notice how some properties are shared – for instance the distance the ball is from the central pole (as you would expect – think about it, they’re both showing the same thing!). When you, now depicted as a smaller blue circle containing a 1 (track mind?... Hur hur, poor show, sorry)), observe the perfectly calculated throw, you see the ball take a more direct route back to you after rebounding off the floor [Small Blue Circle(1)]. In the Right Hand picture, this rebound [Small Red Cricle(2)], appears to travel a much shorter distance – and faster. It can be seen that the time taken for the ball to actually bounce back to you ([Smiley Face(3)] at this point) is way shorter – as it is essentially travels against the direction of the carousel, combining their two velocities.
Quick geek aside: the reason the ball appears to curve in the left hand picture is NOT DUE TO CENTRIFUGAL FORCE. This force does not exist, Newton explained this. It is in fact merely how something moving in a straight line looks to someone who is rotating. However, it is still referred to as it helps massively in thinking about these things, but always remember it is not a real force. It is useful for working things out in the Left Hand diagram – there is a ‘centrifugal force’ pushing all objects outward from the centre of rotation. But the right hand diagram demonstrates it is just a reaction to the centripetal force. The centripetal force is that which makes sure objects moving in a circle, remain in a circle – which is no easy feat, it requires constant force. A Conker on a string, swing it round – why doesn't it fly off? The string of course. But what is the Physical mechanism to describe it? The centripetal force is pulling back on the conker (manifesting itself as the tension in the string). Think of it in this sense, it’s what stops fast spinning things flying off into space and hitting someone in the eye, but it’s not magic – it only works through a physical connection e.g. a string in this case. Geek note number 2: Acceleration as it is defined in science means a change in velocity. Velocity strictly means a speed AND a direction. So because a conker is spinning, even at a constant rate – like a record spinning at 45 RPM, each point on that record is actually experiencing acceleration as its direction is constantly changing. It wants to fly off on a straight path but is held in place by something.
Is the centripetal force required to hold an object of mass ‘m’ in a circular path of radius ‘r’, where one revolution takes T seconds. Also note that takes no consideration of gravity or air resistance for things like conkers. It is useful for calculating the mass of a satellite you’d need to build if you wanted it to remain at a constant altitude and rotate with a constant time period (e.g. geostationary satellites – sit over the same spot on the Earth, orbiting at exactly the same rate).
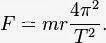 |
| Figure 3: Formulation for centripetal force (m = mass, r = radius of circle that the mass is moving around, T is the time it takes for one revolution of the circle, or the period. |
Long. Geek aside over. Basically, Gauge theory as applied to the quantum world is done under the proviso of something called the Lagrangian being invariant within the system. The Lagrangian is actually a very old classical physics mechanics principle – that effectively quantifies the Principle of Least Action (which goes all the way back to Ancient Greece!) it seems kind of obvious now but nature always takes the shortest path to do anything in the physical world. This happens to be because nature and the natural world are subject to the laws of physics, but this stumped philosophers for centuries – why does the apple fall straight down from the tree? Not do a somersault and fly off into someone’s face? "Nature is thrifty in all its actions" - Pierre Louis Maupertuis. Haha, great quote. Anyway, this developed into the idea of Potential Energy (Euler) who basically said that a system of bodies at rest will adopt a configuration that minimizes total potential energy. Potential energy, something he called ‘effort’ is how much energy is required to do some Work. Again, work here has a very specific meaning in physics – it is the application of an amount of force in a certain amount of time. Applying Force to something is essentially giving something a push (or a pull), essentially executing some kind of mechanical action on a mass that makes it accelerate. Acceleration as we discussed earlier is either changing the speed or direction of an object. An object at rest has zero speed and as such no direction. So the act of moving anything is effectively to make it accelerate, even if it’s just moving a broken down car a few centimetres, there is acceleration involved in making it move even if it doesn’t feel like it lol. So a classic example is lifting an object up a certain distance.
Classic equation, Newton’s Second Law of Motion: F = ma
The Force (F) required to lift an object (against gravity) is mass (m) * gravitational acceleration (a), which is 9.8m/s2 at the Earth’s surface. So for listing 1 kg by 1 metre it would be 1kg * 9.8m/s2 * 1m = 9.8N. N stands for Newtons (unit of Force) and actually reading that back, that statement is essentially meaningless without the idea of time attached – i.e. how long it takes you to lift the mass. I’m gonna do what all science teachers do and just use 1 for everything to keep it simple, so we lift a 1kg block 1 metre in 1 second, that requires 9.8 * 1 * 1 * 1 = 9.8J of energy. J stands for Joules, and it is energy now because some work has been done on the object – i.e. it has moved (a distance 1m), against a force (gravity, 9.8m/s2) in a time (1 second). That’s the same kind of Joules as you see on food and drink nutritional information, except they’re all in kJ, i.e. 1000J. So this can of coke in front of me has 594,000J in it.
Seems like a lot? It is… But then the human body takes a very large amount of Joules to operate. If 1 kcal (food measurement) is 4.2kJ, then recommended RDA of a Male Human – 2500kcals = 10500kJ or 10.5 million Joules. And that’s essentially breaking even.
So back to the Lagrangian – which updated this idea of potential energy, by saying that in any given system, the Lagrangian is the kinetic energy (T) minus the potential energy (V):
L = T – V
No idea why they’re T and V, but the dude put his name to the bloody metric. Imagine if Energy was called Joule, “Allow it blud, she is bare joule’. No doesn’t work, that’s probably why nobody’s heard of the Lagrangian. The thing is, for a classical system it’s not too hard to work it out (not trivial, but providing you know enough it’s a fairly mechanistic process), like for a ball being thrown. Measure it’s speed, position and direction at a few places and you can fill in the blanks with this idea of the ‘Principle of Least Action’, because:
L = T – V
No idea why they’re T and V, but the dude put his name to the bloody metric. Imagine if Energy was called Joule, “Allow it blud, she is bare joule’. No doesn’t work, that’s probably why nobody’s heard of the Lagrangian. The thing is, for a classical system it’s not too hard to work it out (not trivial, but providing you know enough it’s a fairly mechanistic process), like for a ball being thrown. Measure it’s speed, position and direction at a few places and you can fill in the blanks with this idea of the ‘Principle of Least Action’, because:
Kinetic Energy = ½mv2
(Gravitational) Potential Energy = mgh
m is the mass of the ball, v is the velocity (speed and direction), g is the gravitational acceleration (9.8m/s2 ) and h is the height of the ball in metres – gravitational potential energy is determined by the height, an object at a great height has a rather large amount of potential energy, like a bird doing a poo – or perhaps more importantly, a penny being chucked off the top of the Empire State Building. Bird poo is fairly soft and as such the collision is not particularly ‘inelastic’ so it probably won’t kill you. Potential energy is pretty much always gravitational as it’s the main force we have to overcome on Earth, its different when there are springs and bungee cords involved but you get the idea.
Although Lagrange didn’t see his equations being used beyond mechanical applications, it’s quite a deep concept and was applied to quantum mechanics. This is because it’s very generalizable, not one co-ordinate system has to be used, so the space which the Lagrangian defines can be bespoke for the problem at hand – i.e. only describes spacetime co-ordinates that satisfy the constraints of the system. Also if the Lagrangian is symmetrical then all equations derived from it are also symmetrical. In Quantum Mechanics; symmetry, invariance and conservation laws are fundamentally important. As an aside from me: the Quantum world is so beyond our experience, that fastidiously holding on to these basic principles of physics seems like a sort of ‘only beacon in a storm’ type of plan, and has basically caused massive arguments – but ultimately they’ve pretty much all survived (these fundamentals) so they might make a good compass after all. After all, they kind of transcend even mathematics as principles – brand new notation needed to be created, different rules applied, but moving from classical physics, mechanics and engineering principles to quantum theory is like (I imagine) living my life until now, and then suddenly moving to Japan.
It’s full of crazy new ideas and expressions: unitary groups being one in quantum field theory. Group theory is fantastic; a group is a set of elements and an associated operationthat combines any two of its elements into a third element also in the set. It also has to satisfy the four ‘group axioms’:
- Closure: For all a, b in G, the result of the operation, a • b, is also in G
- Associativity: For all a, b and c in G, (a • b) • c = a • (b • c).
- Identity: There exists an element e in G, such that for every element a in G, the equation e • a = a • e = a holds. Such an element is unique (see below), and thus one speaks of the identity element.
- Invertibility: For each a in G, there exists an element b in G such that a • b = b • a = e, where e is the identity element.
An ‘operation’ as mentioned is essentially defined implicitly in the definition of a ‘group’given above; it is a calculation involving 2 elements of a set (in this case called a group) that produces a result that is an element of the set (group).
This definition is quite broad when considered – operations could be elementary arithmetic (addition, subtraction, multiplication, division) and the group could be the set of all real numbers (ℝ). Anyway, group theory is essentially a meta-level of mathematics, certainly in relation to everyday (taught in school) mathematics such as algebra and calculus, and categorises different types of maths into groups.
The groups can have special features asides from adhering to the four axioms (lol). One of which is Symmetry. Another is a Lie group, they describe the symmetries of continuous geometric and analytical structures. Analysis on these and other groups is called harmonic analysis. According to a woman called Noether (good name, this is really weird and I think I might be the first person to notice this – she was born in 1882, and in 1887 Michelson & Morley did their famous experiment that disproved the existence of the luminiferous aether (or ‘ether’) – a medium for electromagnetic propagation). That was a huge deal back then – it was universally accepted there must be a medium for light to propagate through) stated that ANY symmetry in a physical system has a corresponding conservation law. Essentially, by defining a Quantum Field System as a Lie group, with continuous (read – infinite) symmetries, it must conserve all the important aspects: Energy, Centre of Momentum, Conformal Transformation, Electric Charge and all the other conservations that physicists care about. That was a massive simplification but that’s how Quantization works (turning a classical system into a quantum system), by summing over infinite possibilities in a system – the Lagrangian could be one of many (read – infinite) things according to probability distributions and so after some highly debated maths, where lots of ‘infinities’ are cancelled with each other, you reach these conservation equations that are at the heart of Quantum Field Theory.
Remember awhile back I talked about the Electroweak Force – a force that exists only at temperatures (energy) high enough that the electroweak symmetry remains unbroken – upon breaking it forms the Electromagnetic force and the Nuclear Weak force, 2 of the fundamental forces in particle physics, that are actually rather different. At a critical temperature, the Higgs field becomes Tachyonic (oh dear) and the Symmetry is spontaneously broken, and Tachyon condensation occurs – the Higgs boson is released, and interacts with two other bosons (W and Z by name) that then acquire mass as that is what old Higgs boson does. In some versions of this condensation, the excitations (particles) decay into another, stable configuration with no Tachyons. In some they don’t, and this can cause a cascade of condensation that will travel throughout the entire ‘future light cone’ of the Tachyon – thus propagating through the Universe, and very likely this is what happened and why we have the EM force and the Nuclear Weak force today.
So, time-travel… Tachyons – no, basically, although they did make the world how it is today and sorts out a lot of the maths surrounding anything propagating faster than the speed of light in Quantum Field Theory – in that it pretty much just condenses.
Gödel’s CTC’s – not really, as the solution for the Theory of Relativity here appears to require the Universe to have physical characteristics it does not have (the Hubble constant – now known to a high degree of accuracy, does not allow it).
The ‘wormhole’ is another great namedrop in time travel mythology, and has surprisingly robust mathematics behind it. Certainly according to Einstein’s General ToR there are valid solutions that contain wormholes. The issues are:
- Creating one (they don’t seem to appear naturally)
- Keeping it open long enough to travel through
- Making it large enough for anything larger than a photon to pass through
First let’s be clear on what one is – it’s a tunnel produced by warping spacetime in such a drastic way that it sort of bends in on itself until it becomes disconnected from its consecutive spacetime neighbours and joins with another, unknown, area of spacetime. This would allow matter and energy to pass through as easily as walking through a door – creating a shortcut from one area of spacetime to another.
There are also multiple theories about wormholes – involving different solutions to the old General ToR. Two of the top interpretations of GoR (Schwarzschild metric and Einstein–Cartan–Sciama–Kibble theory of gravity) provide for wormholes in black holes. The former interpretation suggests that if a large enough mass undergoes gravitational collapse, it forms a singular ‘Schwarzschild’ black hole, that is effectively a one-way path to another Universe that exists within the black hole. In the latter interpretation – the collapse forms a ‘regular’ black-hole (Einstein–Rosen bridge), as the intrinsic ‘spin’ of matter at such high densities as would be found in a black hole would repel each particle away, preventing an actual gravitational singularity – remaining at an enormous (but finite) density, and then rebounds out the other side, forming the other side of the bridge.
So problem a) is perhaps not as serious as first thought – indeed the ‘quantum foam’ theory (linked to the ephemeral particles appearing and disappearing all the time in space) says tiny wormholes blink in and out of existence all the time.
Pragmatically, some kind of new technology or material is going to be needed to do something useful with these black hole/wormhole ideas – and there is a lot of mention of ‘exotic matter’ (even by Hawking) that may possess negative energy. All this being said and done, with this exotic matter and high tech in hand, building one entrance to a wormhole is only the start (literally). It would never be possible to travel back to a time earlier than when the wormhole was first created.
Hawking is a loose cannon on this – I think he really wants there to be wormholes. Maybe it’s his pension plan. He claims the Casimir Effect demonstrates the existence of the exact type of exotic matter that would be required to stabilize a worm hole so it was traversable. However, it’s all conjecture.
Basically nobody REALLY knows, until they sort out the full theory of quantum gravity, which might take awhile. The closest we’ll get in terms of today’s thinking is with time dilation, and quantum entanglement, meaning perhaps latency free communication with spaceships light years away, but no beaming up just yet.
Cheers,
Duncan